Skip to contents

Create a skeleton of a closed polygon object

Source: R/cnt_skeleton.R
cnt_skeleton.Rd

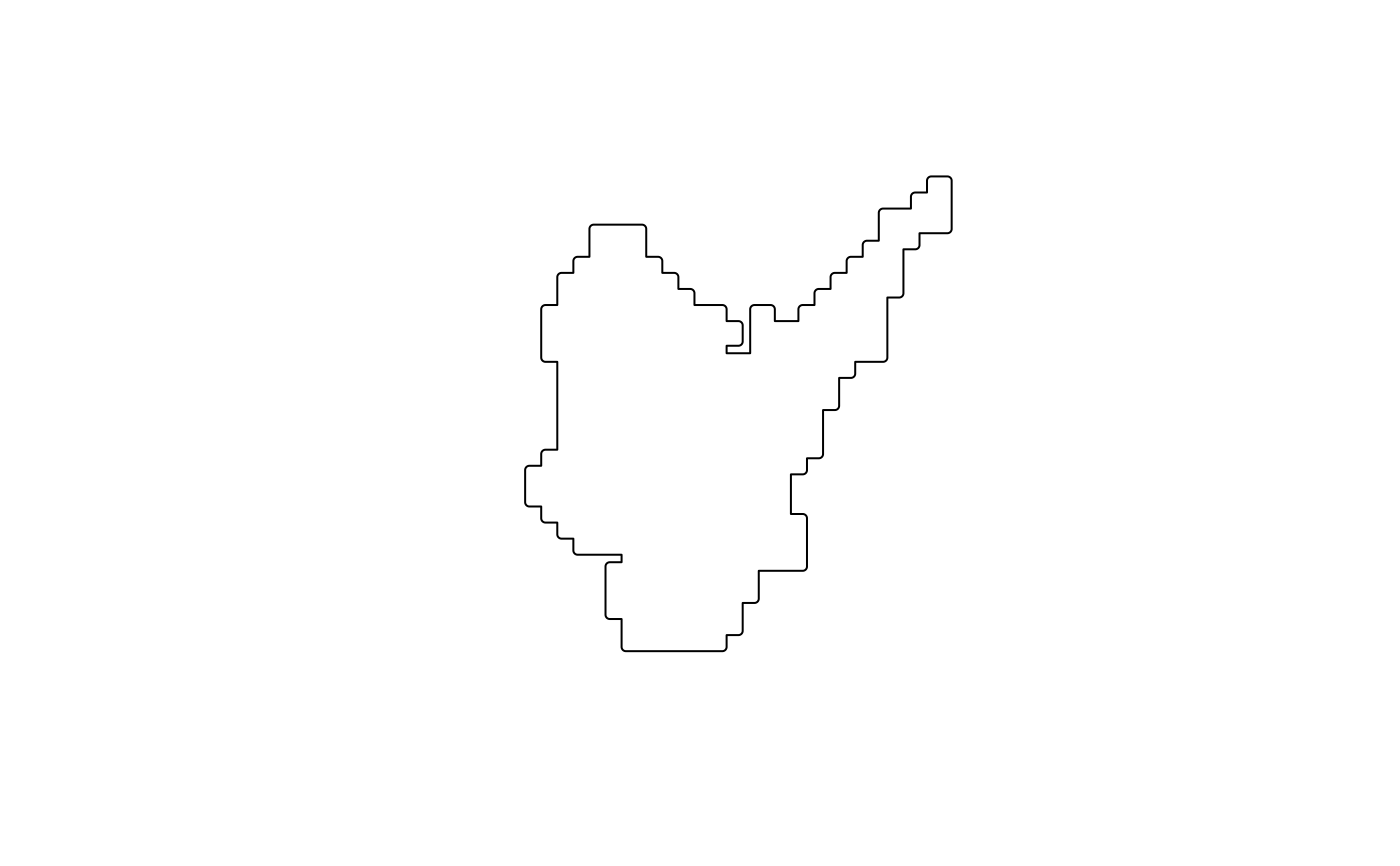
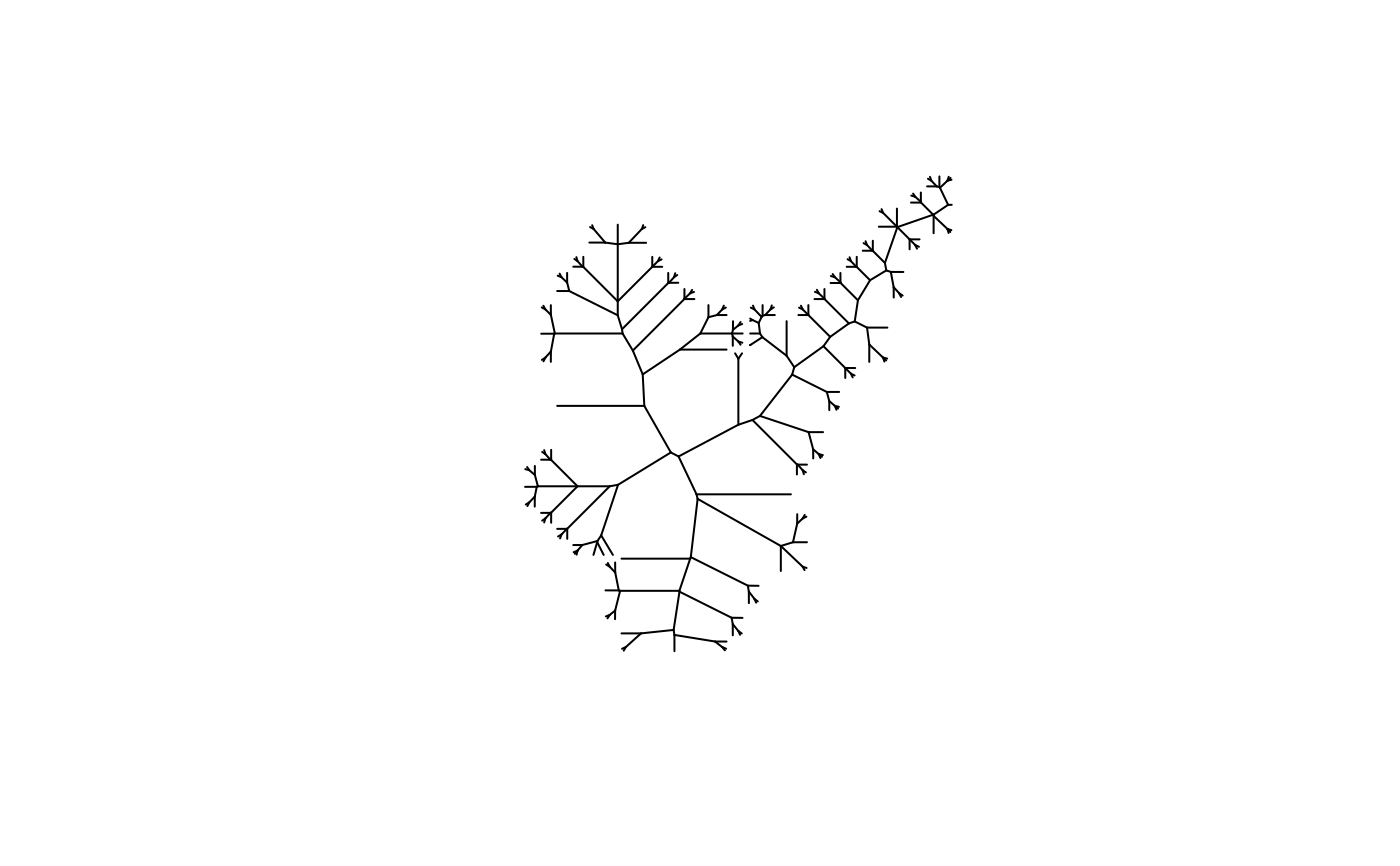
This function generates skeletons of closed polygon objects.

Usage

cnt_skeleton(input, keep = 0.5, method = "voronoi")

Arguments

input

sf, sfc, SpatVector, or geos_geometry polygons object

keep

numeric, proportion of points to retain (0.05-5.0; default 0.5). See Details.

method

character, either "voronoi" (default) or "straight", or just the first letter "v" or "s". See Details.

Value

a sf, sfc, SpatVector or geos_geometry class object of a MULTILINESTRING geometry

Details

Polygon simplification/densification

  • If keep = 1, no transformation will occur. The function will use the original geometry to find the skeleton.

  • If the keep parameter is below 1, then the geos::geos_simplify() function will be used. So the original input geometry would be simplified, and the resulting skeleton will be cleaner but maybe more edgy. The current realisation of simplification is similar (but not identical) to rmapshaper::ms_simplify() one with Douglas-Peuker algorithm. However, due to geos superpower, it performs several times faster. If you find that the built-in simplification algorithm performs poorly, try rmapshaper::ms_simplify() first and then find the polygon skeleton with keep = 1, i.e. cnt_skeleton(rmapshaper::ms_simplify(polygon_sf), keep = 1)

  • If the keep is above 1, then the densification algorithm is applied using the geos::geos_densify() function. This may produce a very large object if keep is set more than 2. However, the resulting skeleton would potentially be more accurate.

Skeleton method

  • If method = "voronoi" (default), the skeleton will be generated using the geos::geos_voronoi_edges() function. This is application of the Voronoi diagram algorithm (Voronoi, 1908). A Voronoi diagram partitions space into regions based on the distance to the polygon's vertices. The edges of these cells form a network of lines (skeletons) that represent the structure of the polygon while preserving its overall shape.

  • If method = "straight", the skeleton will be generated using the raybevel::skeletonize() function. See https://www.tylermw.com/posts/rayverse/raybevel-introduction.html

References

Voronoi, G. (1908). Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Journal für die reine und angewandte Mathematik, 134, 198-287. doi:10.1515/crll.1908.134.198

Examples

library(sf)

polygon <-
  sf::st_read(system.file("extdata/example.gpkg", package = "centerline"),
    layer = "polygon",
    quiet = TRUE
  )

plot(polygon)


pol_skeleton <- cnt_skeleton(polygon)

plot(pol_skeleton)